Gambar 4. Vektor pada koordinat kartesius dimensi tiga
Dalam ruang-ruang
dimensi tiga suatu titik dinyatakan dengan tiga komponen, yaitu absis, ordinat
dan aplikat. Misalnya B(x1, y1, z1). Vektor posisi
(terhadap titik O) untuk titik B adalah a
= < x1, y1, z1> = x1i, y1j, z1k.
Vektor-vektor basis i,j,k berturut-turut adalah
vektor-vektor satuan yang searah dengan sumbu-sumbu x positif, y positif dan z
positif.
Semua sifat penjumlahan
vekotr dan perkalian vekotr dengan skalar yang berlaku dalam bidang datar juga
berlaku untuk vektor dalam ruang dimensi tiga.
PANJANG VEKTOR
Jika a = < x1, y1, z1>
maka panjang vektor a adalah,
PERKALIAN TITIK PADA VEKTOR
Jika u = < u1, u2, u3>
dan v = < v1, v2,
v3>, maka perkalian titiknya didefinisikan sebagai berikut
Dengan θ adalah sudut
yang dibentuk oleh u dan v dan serta 0 ≤ θ ≤ phi
Dari definisi diatass
didaptkan rumus sudut yang dibentuk oleh vektor u dan v yaitu,
PERKALIAN VEKTOR
Jika u = < u1, u2, u3>
dan v = < v1, v2,
v3> maka perkalian kedua vektor adalah,
HASIL KALI SILANG DUA VEKTOR
Perkalian silang dua vektor a = a1i + a2j + a3k
dan b = b1i + b2j + b3k
didefinisikan sebagai berikut,
Dengan θ adalah sudut
yang dibentuk kedua vektor dan u adalah
vektor satun yang tegak lurus pada a dan
b.

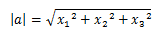




Tidak ada komentar:
Posting Komentar